サンプリングにおける加速と安定性

発表概要

PDMP とはマルコフ連鎖，拡散過程に続いて，近年活発にモンテカルロ法に利用されつつある連続時間マルコフ過程のクラスである．より速く収束するサンプラーが構成しやすいこと，モンテカルロ推定量にバイアスを導入しないようなサブサンプリング（バッチ実行）が可能であることから，近年特に統計・機械学習の分野でも注目が高まっている．

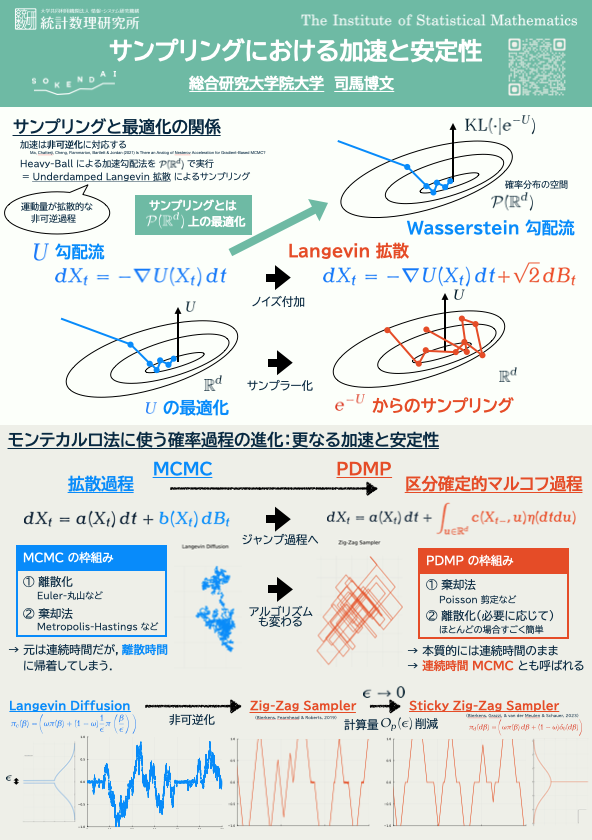
本ポスターではまず，サンプリングと最適化の関係を図によってまとめる．目的関数を \(\newcommand{\R}{\mathbb{R}}U:\R^d\to\R\) で表すと，その勾配流 \(\dot{x}=-\nabla U(x)\) に確率的な揺らぎを加えた過程である Langevin 拡散過程 \[ dX_t=-\nabla U(X_t)\,dt+\sqrt{2\beta^{-1}}\,dB_t \] による確率分布 \(\pi(x)\propto e^{-U(x)}\) からのサンプリングは，\(\mathcal{P}(\R^d)\) 上の勾配流の離散化だと見れる (Bernton, 2018), (Durmus ほか, 2019), (Wibisono, 2018), (Zhang と Nemeth, 2024)．このときの目的関数は KL 乖離度 \(F(\rho):=\operatorname{KL}(\rho,e^{-U})\) である．

近年 Langevin 拡散過程のような古典的なサンプラーを改善する試みが MCMC の理論・手法研究で進んでいる．キーワードの一つが 非可逆性 である．Langevin 拡散を非可逆化した代表的なダイナミクスには underdamped Langevin diffusion というものが存在する： \[ \begin{cases} dX_t=V_t\,dt,\\ dV_t=-(\nabla U(X_t)+\gamma V_t)\,dt+\sqrt{2\gamma}\,dB_t. \end{cases} \tag{1}\]

この underdamped Langevin diffusion の離散化によるサンプラーには GHMC (Generalized Hamiltonian Monte Carlo) (Horowitz, 1991) が存在し，現在の（ほとんど）SOTA である HMC を大きく改善する．が，シミュレーション技術に問題があり，アルゴリズムとしての tuning-free 化に苦しんでいる (Hoffman と Sountsov, 2022)．

Underdampled Langevin dynamics (1) は実は (Polyak, 1964) による Heavy-Ball 加速勾配法の連続極限と \(dB_t\) の項を除いて一致する．すなわち，MCMC の界隈で理解されている「非可逆化によるサンプラーの加速」は，最適化の言葉では加速法として理解できるのである．この (Ma ほか, 2021) の観察を紹介する．

非可逆なダイナミクスを持つ MCMC サンプラーとして期待されている手法は GHMC だけでない．PDMP (Piecewise Deterministic Markov Process) というクラスの Markov 過程に基づく，新種の MCMC 手法が近年提案されている (Fearnhead ほか, 2018)．

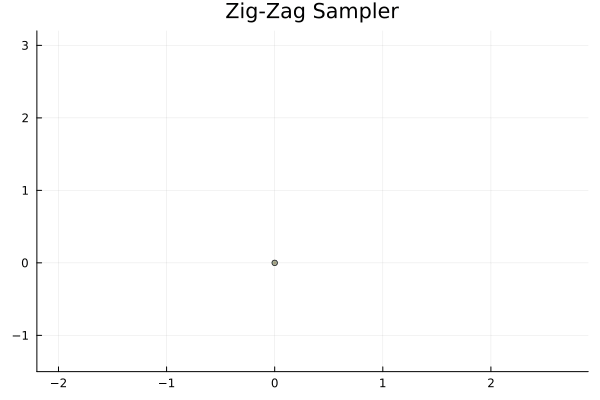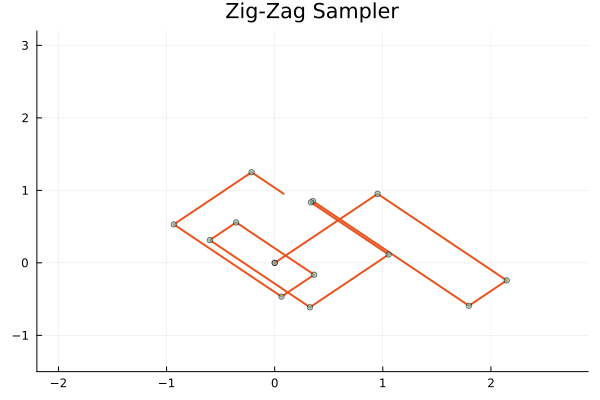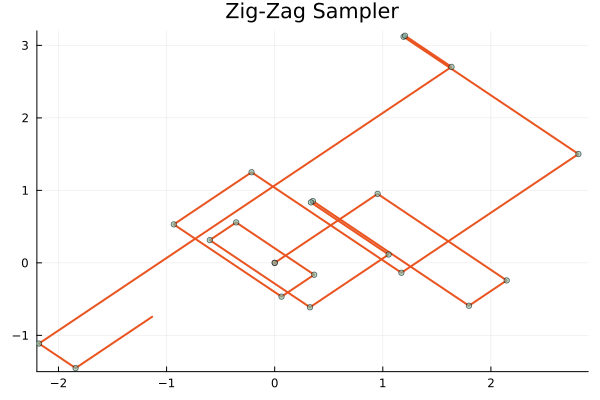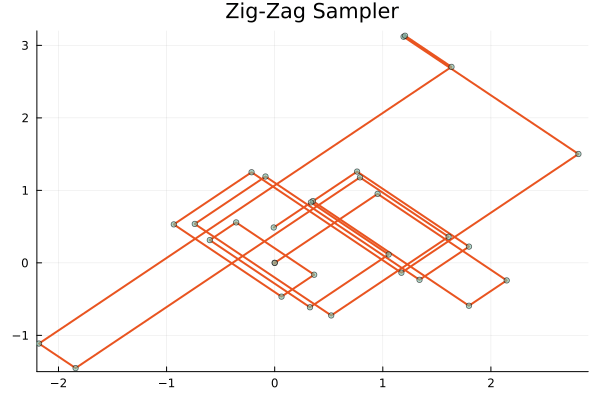
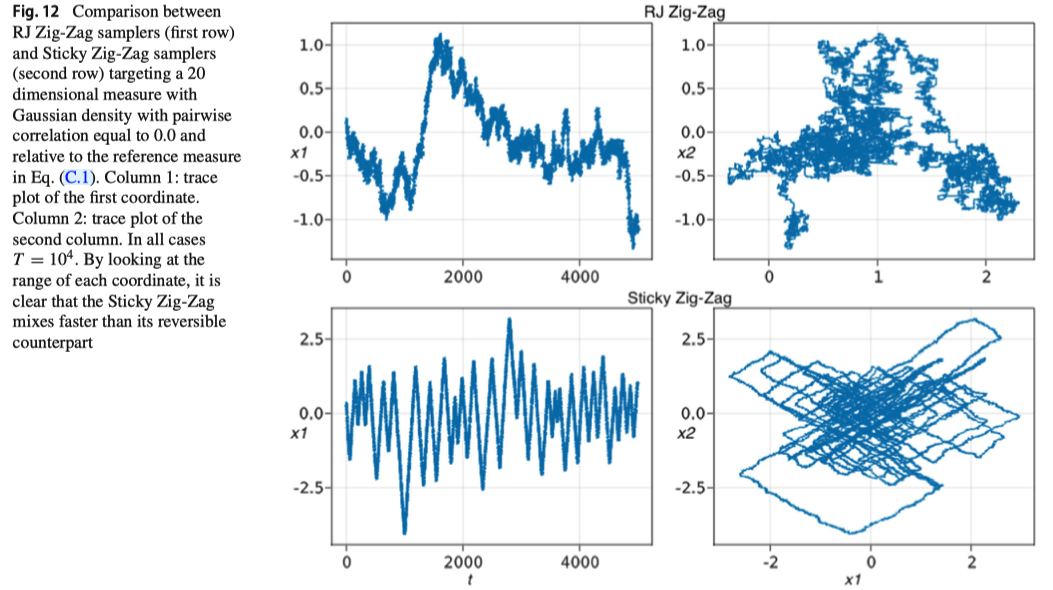
本ポスターでは最後に，「 \(\delta_x\) 部分を持った非絶対連続確率分布からも正確なサンプリングが可能」という PDMP に基づくモンテカルロ法の第３の美点に焦点を当てる． PDMP 法と従来法との挙動の違いを調べるために，スパイク幅が \(0\) に収束する極限という従来考えられなかったレジームを導入する．

このレジームにおいて，従来法はスパイクの検出に失敗し，誤った分布からサンプリングを行ってしまう． 一方で PDMP 法はスパイクの台への到達確率が \(0\) でない限り，正しい分布からサンプリングを行うことができる．

加えて極限もまた別の PDMP となり，これを直接シミュレートすることで，\(\delta\) 部分を持った非絶対連続分布からの効率的なサンプリングが可能になる． なお，この極限で得られるサンプラーは Sticky PDMP (Bierkens ほか, 2023) と一致する．

連続最適化および関連分野に関する夏季学校

Date	Location
Aug. 28th - 30th, 2025	統数研２階大会議室

画像をクリックで PDF を表示

参考ページ集

PDMP とそのシミュレーションに関しては，次のスライドにわかりやすく解説されています：

図は全て発表者開発のパッケージ PDMPFlux.jl によるものです．

Sticky PDMP (Bierkens ほか, 2023) に関するさらに詳しい内容，またはベイズ変数選択一般については，次の記事にまとめています：

参考文献

Bernton, E. (2018). Langevin Monte Carlo and JKO splitting. S. Bubeck, V. Perchet, と P. Rigollet, 編, Proceedings of the 31st Conference On Learning Theory,Vol. 75, ページ 1777–1798. PMLR.

Bierkens, J., Grazzi, S., Meulen, F. van der, と Schauer, M. (2023). Sticky PDMP Samplers for Sparse and Local Inference Problems. Statistics and Computing, 33(1), 8.

Durmus, A., Majewski, S., と Miasojedow, B. (2019). Analysis of Langevin Monte Carlo via Convex Optimization. Journal of Machine Learning Research, 20(73), 1–46.

Fearnhead, P., Bierkens, J., Pollock, M., と Roberts, G. O. (2018). Piecewise Deterministic Markov Processes for Continuous-Time Monte Carlo. Statistical Science, 33(3), 386–412.

Hoffman, M. D., と Sountsov, P. (2022). Tuning-Free Generalized Hamiltonian Monte Carlo. G. Camps-Valls, F. J. R. Ruiz, と I. Valera, 編, Proceedings of The 25th International Conference on Artificial Intelligence and Statistics,Vol. 151, ページ 7799–7813. PMLR.

Horowitz, A. M. (1991). A generalized guided Monte Carlo algorithm. Physics Letters B, 268(2), 247–252.

Ma, Y.-A., Chatterji, N. S., Cheng, X., Flammarion, N., Bartlett, P. L., と Jordan, M. I. (2021). Is there an analog of Nesterov acceleration for gradient-based MCMC? Bernoulli, 27(3), 1942–1992.

Polyak, B. T. (1964). Some methods of speeding up the convergence of iteration methods. USSR Computational Mathematics and Mathematical Physics, 4(5), 1–17.

Wibisono, A. (2018). Sampling as optimization in the space of measures: The Langevin dynamics as a composite optimization problem. S. Bubeck, V. Perchet, と P. Rigollet, 編, Proceedings of the 31st Conference On Learning Theory,Vol. 75, ページ 2093–3027. PMLR.

Zhang, R.-Y., と Nemeth, C. (2024). Why Should We Care About Gradient Flows?: Blog post on gradient flows in Euclidean and Wasserstein spaces.