メトロポリスを超えた枠組みで我々はどこまで行けるか？

発表概要

区分確定的マルコフ過程 (PDMP: Piecewise Deterministic Markov Process) に基づく Monte Carlo 法は，Metropolis-Hastings (MH) の枠組みから逸脱することでスケーラビリティを達成する MCMC 手法である．良いサーベイは (Fearnhead+2018-PDMC?) など．

より速い収束 (Andrieu と Livingstone, 2021) に加え，ミニバッチから計算した勾配の不偏推定量のみを用いて実行した場合も漸近的に正確な推論が可能であることが美点である．この点，Stochastic Gradient (Ma ほか, 2015) と特に相性が良いと言える．

しかし，momentum を用いる方法 (Horowitz, 1991) や自然勾配 (Girolami と Calderhead, 2011) を用いる方法など，従来 MH 法に対して培われた性能改善手法はそのままでは PDMP に使えない．

その中で，PDMP の性能を持続的な運動量を保持する技術を備えた Forward Event-Chain Monte Carlo 法 (Michel ほか, 2020) という手法が，PDMP の枠組みの中で尤度の幾何的情報を上手に利用して収束を速める・計算複雑性を低減できているということを，スケーリング解析による Bouncy Particel Samper (Bouchard-Côté ほか, 2018) との比較を通じて示す．

Information-Based Induction Sciences Workshop (IBIS2025)

Date	Location
Nov. 12-15, 2025	那覇文化芸術劇場なはーと

画像をクリックで PDF を表示

参考ページ集

PDMP とそのシミュレーションに関しては，次のスライドにわかりやすく解説されています：

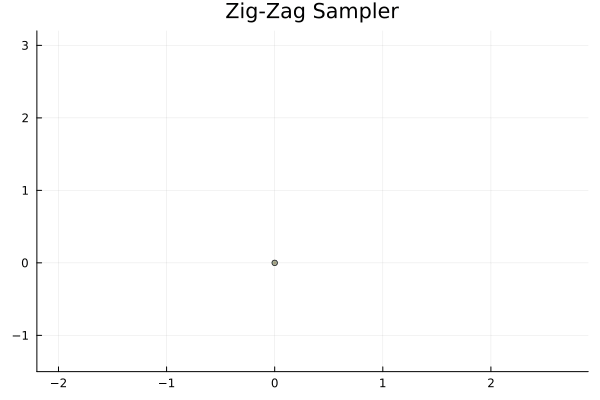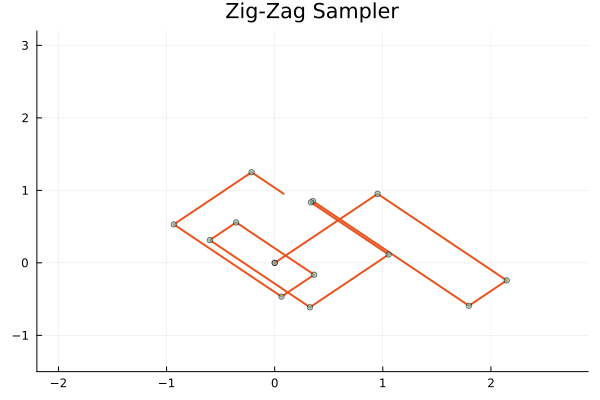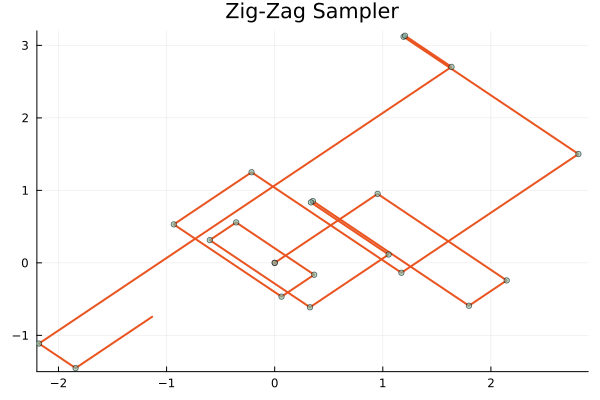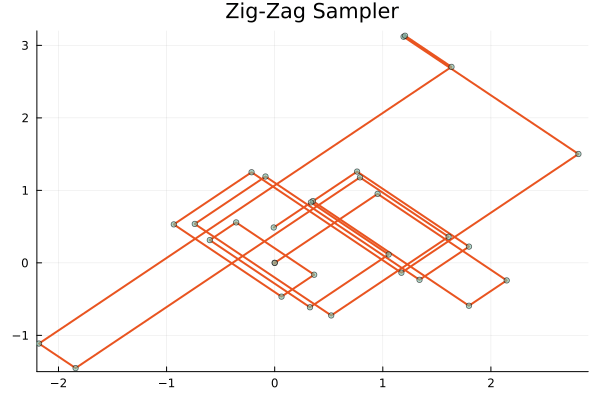
図は全て発表者開発のパッケージ PDMPFlux.jl によるものです．

Sticky PDMP (Bierkens ほか, 2023) に関するさらに詳しい内容，またはベイズ変数選択一般については，次の記事にまとめています：

参考文献

Andrieu, C., と Livingstone, S. (2021). Peskun–Tierney ordering for Markovian Monte Carlo: Beyond the reversible scenario. The Annals of Statistics, 49(4), 1958–1981.

Bierkens, J., Grazzi, S., Meulen, F. van der, と Schauer, M. (2023). Sticky PDMP Samplers for Sparse and Local Inference Problems. Statistics and Computing, 33(1), 8.

Bouchard-Côté, A., Vollmer, S. J., と Doucet, A. (2018). The Bouncy Particle Sampler: A Nonreversible Rejection-Free Markov Chain Monte Carlo Method. Journal of the American Statistical Association, 113(522), 855–867.

Girolami, M., と Calderhead, B. (2011). Riemann manifold Langevin and Hamiltonian Monte Carlo methods. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 73(2), 123–214.

Horowitz, A. M. (1991). A generalized guided Monte Carlo algorithm. Physics Letters B, 268(2), 247–252.

Ma, Y.-A., Chen, T., と Fox, E. (2015). A Complete Recipe for Stochastic Gradient MCMC. C. Cortes, N. Lawrence, D. Lee, M. Sugiyama, と R. Garnett, 編, Advances in Neural Information Processing Systems,Vol. 28. Curran Associates, Inc.

Michel, M., Durmus, A., と Sénécal, S. (2020). Forward Event-Chain Monte Carlo: Fast Sampling by Randomness Control in Irreversible Markov Chains. Journal of Computational and Graphical Statistics, 29(4), 689–702.